Motivation
A multi dimensional lookup table is present in nearly every ICC profile. But they can be adopted also in other situations, for example where the color conversion is expensive to compute and may be useful to turn a generic function_t<Y, X>, build from the composition of several steps, into a single N- dimensional table with precomputed values on grid and then make use of interpolation for intermediate values. This library has the components to make this task easy, can be applied to dimensions bigger than three, and can use both multi-linear and tetrahedral interpolation. After all this advertising let’s start to give a look at how this is implemented.
The core class
This is the man class, I just stripped off a the trivial parts like the cloning function. The eval(const X &x) const function first of all finds the cube/square/element where x stays. This is used to fill in the delta vector and in this way the funcion has paid its dependency on input space by turning all into a vector. Then the result is handed to the data_ object that holds the grid points to make the interpolation. This part is a weighted sum of the grid points, and so the output space has to implement the mutiplication by a scalar and addition. That’s straightforward for floating point types, requires an extra trick when one has to deal with unsigned char
template
class lut_t : public algo_t
{
public:
enum {dimension = X::dimension};
lut_t(const size_t *size, const X &step) :
data_(size), step_(step) {}
virtual Y eval(const X &x) const override
{
delta_item_t deltas[dimension];
// find the cube x belongs (and the remainders)
input_traits_t::split(x,
step_,
deltas,
data_.size1());
// build the interpolation
return data_.combine(deltas, I());
}
private:
arrayn_t data_; // TODO: consider
X step_; // sharing this data..
};

But now it’s time to see how the split is done. To make things simple to follow I will describe the 2D case, but the reasoning can be extended to any dimension. On the plane the multi-dimensional lookup table is a unit square with each side divided in N parts. The function has been evaluated at each corner of the grid. Given a generic point P(x,y) the first thing to do is to find out to which sub-square it falls in. That’s quit easy: just divide each coordinate by the side of the sub-square. The integer part will be the index (xi) for that dimension and the remainder (dx) will be related to the weights to interpolate the table values next to it.
Before carrying on let me stress again that this operation (finding the indexes and remainders) is dependent on the type of the input space. Is a single concept that needs to be implemented in a way if the input space is an N-dimensional vector, and in another if input space is e.g. rgb. The library defines a trait class for this operation, and provides (at the moment) two implementation: one for rgb and one for the vector template. They have been crafted carefully, so they work both for floating point types and for integer types like rgb_t<unsigned char>.
This is the code for the rgb_t case. The scalar_traits::one() function returns 1.0 for floating point types, and returns 255 for unsigned char.
template
struct lut_input_traits_t<rgb_t>
{
typedef T scalar_type;
typedef typename scalar_traits_t::weight_type weight_type;
static void split(const rgb_t &x,
const rgb_t &step,
delta_item_t *deltas,
const size_t *size1)
{
split_0(x.red, step.red, deltas, size1);
split_0(x.green, step.green, deltas + 1, size1 + 1);
split_0(x.blue, step.blue, deltas + 2, size1 + 2);
}
static void split_0(T x, T step,
delta_item_t *deltas,
const size_t *size1)
{
T div = x / step;
deltas->offset = static_cast(div);
deltas->offset -= deltas->offset / size1[0];
// deltas->value = x - deltas->offset * step;
deltas->value = x * scalar_traits_t::one() / step -
deltas->offset * scalar_traits_t::one();
}
};
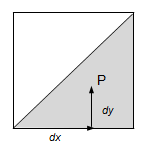
At this point if we want to do a multi-linear interpolation is all quite ready. But if we want to do tetrahedral interpolation (triangular in 2D) then there is another problem: we must find out in which triangle our point falls in. In 2D this is quite simple. If remainder (dx) on x axis is bigger than dy then the point is in the lower triangle (like in the picture on the right), otherwise in the upper. This means that to find the point involved in the interpolation we can do the following: starting from the bottom right corner we increment first the dimension that has the bigger remainder. This is a reasoning that can be easily generalized: if we have a space of dimension N then we take the remainders (dx1, dx2, …dxn) and sort them in decreasing order. I do not have a formal proof of this fact, just the fact that… works (and gives non-negative weights for the values at the vertexes, which is definitely a must).
Below there is the code for this operation. The perm_ object does the sorting. This is an actual sort only for N > 5, otherwise there is another object that evaluates dx[i] < dy[j] for every i < j and builds a sort of 'signature' of the input. For N = 3 this means just 3 comparisons and, more important, this means that the whole operation can be don without a single if instruction. So the processor pipeline of the processor never gets reset and computation is done at the highest possible speed. For values bigger then N the lookup table required starts to grow too much, and I think that a standard sort is better.
template <class Y, int N>
class arrayn_t
{
public:
template <class S> // S is a scalar
Y combine(delta_item_t<S> *deltas, interp_tetra_t) const
{
// computes offset of first cube ans substitutes
// the indexes with offset for each dimension
const Y *data = data_ +
iteration_t<S, N>::substitute(deltas, offset_);
// sort deltas to have them in decreasing order
perm_.indexes(deltas);
// for byte type one() is 256, hence the trait
return data[0] *
(scalar_traits_t<S>::one() - deltas->value) +
voxel_sum_t<Y, S, N>::tetrahedral(data, deltas);
}
private:
size_t size_[N];
size_t size1_[N];
size_t offset_[N + 1];
Y *data_;
permutation_t<N, (N > 5)> perm_;
};
Now we can compute the weighted sum of the points at the vertexes. This means that the type Y must have defined an operator* (multiplication by scalar) and an addition. Then there is a trick for integer types. The trick is that the operator * for rgb_t<unsigned char> gives actually a rgb_t<int> that is later on down-scaled again to rgb_t<unsigned char>. Yes, is a bit tricky, but in this way I have a single implementation for the interpolation, which I consider a Good Thing (TM). Let me know your opinion about that. If you want to see the implementation of this part then look at the soure code. voxel_sum_t is a simple template that unrolls the loop over N.
It has been hard, but at last we have enough tools to read a profile and build a transform. But this will be matter for another post…